Focal Loss

该损失函数由Kaiming大神提出来，一开始是用在目标检测算法中。关于该损失函数的描述大部分内容来自下面参考链接2。

出发点

object detection的算法主要可以分为两大类：two-stage detector和one-stage detector。前者是指类似Faster RCNN，RFCN这样需要region proposal的检测算法，这类算法可以达到很高的准确率，但是速度较慢。虽然可以通过减少proposal的数量或降低输入图像的分辨率等方式达到提速，但是速度并没有质的提升。后者是指类似YOLO，SSD这样不需要region proposal，直接回归的检测算法，这类算法速度很快，但是准确率不如前者。作者提出focal loss的出发点也是希望one-stage detector可以达到two-stage detector的准确率，同时不影响原有的速度。

既然有了出发点，那么就要找one-stage detector的准确率不如two-stage detector的原因，作者认为原因是：样本的类别不均衡导致的。我们知道在object detection领域，一张图像可能生成成千上万的candidate locations，但是其中只有很少一部分是包含object的，这就带来了类别不均衡。那么类别不均衡会带来什么后果呢？引用原文讲的两个后果：(1) training is inefficient as most locations are easy negatives that contribute no useful learning signal; (2) en masse, the easy negatives can overwhelm training and lead to degenerate models. 什么意思呢？负样本数量太大，占总的loss的大部分，而且多是容易分类的，因此使得模型的优化方向并不是我们所希望的那样。其实先前也有一些算法来处理类别不均衡的问题，比如OHEM（online hard example mining），OHEM的主要思想可以用原文的一句话概括：In OHEM each example is scored by its loss, non-maximum suppression (nms) is then applied, and a minibatch is constructed with the highest-loss examples。OHEM算法虽然增加了错分类样本的权重，但是OHEM算法忽略了容易分类的样本。

因此针对类别不均衡问题，作者提出一种新的损失函数：focal loss，这个损失函数是在标准交叉熵损失基础上修改得到的。这个函数可以通过减少易分类样本的权重，使得模型在训练时更专注于难分类的样本。

二分类focal loss定义

focal loss的含义可以看如下Figure1，横坐标是$p_t$，纵坐标是loss。$CE(p_t)$表示标准的交叉熵公式，$FL(p_t)$表示focal loss中用到的改进的交叉熵，可以看出和原来的交叉熵对比多了一个调制系数（modulating factor）。它的目的是通过减少易分类样本的权重，从而使得模型在训练时更专注于难分类的样本。首先$p_t$的范围是0到1，所以不管$\gamma$是多少，这个调制系数都是大于等于0的。易分类的样本再多，你的权重很小，那么对于total loss的共享也就不会太大。那么怎么控制样本权重呢？举个例子，假设一个二分类，样本x1属于类别1的$p_t=0.9$，样本x2属于类别1的$p_t=0.6$，显然前者更可能是类别1，假设$\gamma=1$，那么对于$p_t=0.9$，调制系数则为0.1；对于$p_t=0.6$，调制系数则为0.4，这个调制系数就是这个样本对loss的贡献程度，也就是权重，所以难分的样本$p_t=0.6$的权重更大。Figure1中$\gamma=0$的蓝色曲线就是标准的交叉熵损失。

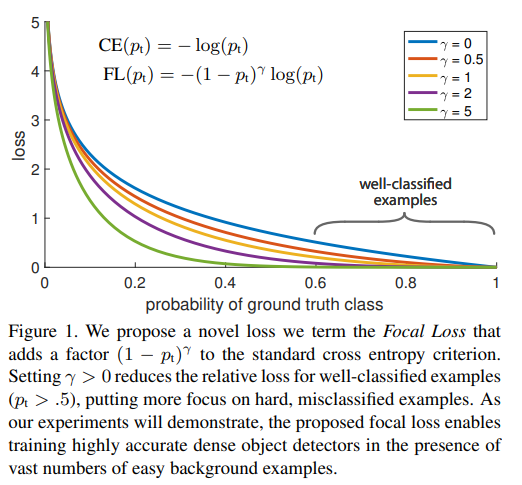
在介绍focal loss之前，先来看看交叉熵损失，这里以二分类为例，$p$表示概率，公式如下：

$$\begin{eqnarray} CE(p,y)=\left\{ \begin{aligned} -log(p) \ \ \ \ \ if \ \ y=1\\ -log(1-p) \ \ \ \ \ otherwise \end{aligned} \right. \end{eqnarray}$$

因为是二分类，所以$y$的值是正1或负1，$p$的范围为0到1。当真实label是1，也就是$y=1$时，假如某个样本X预测为1这个类的概率$p=0.6$，那么损失就是$-log(0.6)=0.5108$。如果$p=0.9$，那么损失就是$-log(0.9)=0.1053$，所以$p=0.6$的损失要大于$p=0.9$的损失。

为了方便，用$p_t$代替$p$与$1-p$，如下面公式，这里的$p_t$即为上面Figure1中的横坐标。

$$\begin{eqnarray} p_t=\left\{ \begin{aligned} p \ \ \ \ \ if \ \ y=1\\ 1-p \ \ \ \ \ otherwise \end{aligned} \right. \end{eqnarray}$$

那么$CE(p,y)$就可以重写为下面式子：

$$\begin{eqnarray} CE(p,y)=CE(p_t)=-log(p_t) \end{eqnarray}$$

论文中首先提到了对交叉熵的最基本改进，作为baseline，如下面公式所示。在原公式的基础上添加了一个系数$\alpha_t$，跟$p_t$的定义类似，当真实label是1，也就是$y=1$时，$\alpha_t=\alpha$；当当真实label是-1，也就是$y=-1$时，$\alpha_t=1-\alpha$。$\alpha$的取值范围也是0到1。因此可以通过设定$\alpha$的值（一般而言假如1这个类的样本数比-1这个类的样本数多很多，那么$\alpha$会取0到0.5来增加-1这个类的样本的权重）来控制正负样本对总的loss的共享权重。

$$\begin{eqnarray} CE(p_t)=-\alpha_tlog(p_t) \end{eqnarray}$$

该公式虽然可以控制正负样本的权重，但是没法控制容易分类和难分类样本的权重，于是就有了focal loss：

$$\begin{eqnarray} FL(p_t)=-(1-p_t)^\gamma log(p_t) \end{eqnarray}$$

这里的$\gamma$称为focusing parameter，$\gamma>=0$。$(1-p_t)^\gamma$称为调制系数（modulating factor）。

性质

focal loss的两个重要性质：

1. 当一个样本被分错的时候，$p_t$是很小的（请结合公式2，比如当$y=1$时，$p$要小于0.5才是错分类，此时$p_t$就比较小，反之亦然），因此调制系数就趋于1，也就是说相比原来的loss是没有什么大的改变的。当$p_t$趋于1的时候（此时分类正确而且是易分类样本），调制系数趋于0，也就是对于总的loss的贡献很小。
2. 当$\gamma=0$的时候，focal loss就是传统的交叉熵损失，当$\gamma$增加的时候，调制系数也会增加。

focal loss的两个性质算是核心，其实就是用一个合适的函数去度量难分类和易分类样本对总的损失的贡献。

而在论文中，作者在做实验时，采用了结合了公式$({4})$和$({5})$的focal loss，这样既能调整正负样本的权重，又能控制难易分类样本的权重

$$\begin{eqnarray} FL(p_t)=-\alpha_t(1-p_t)^\gamma log(p_t) \end{eqnarray}$$

在实验中$\alpha$的选择范围也很广，一般而言当$\gamma$增加的时候，$\alpha$需要减小一点（实验中$\gamma=2，\alpha=0.25$的效果最好）。

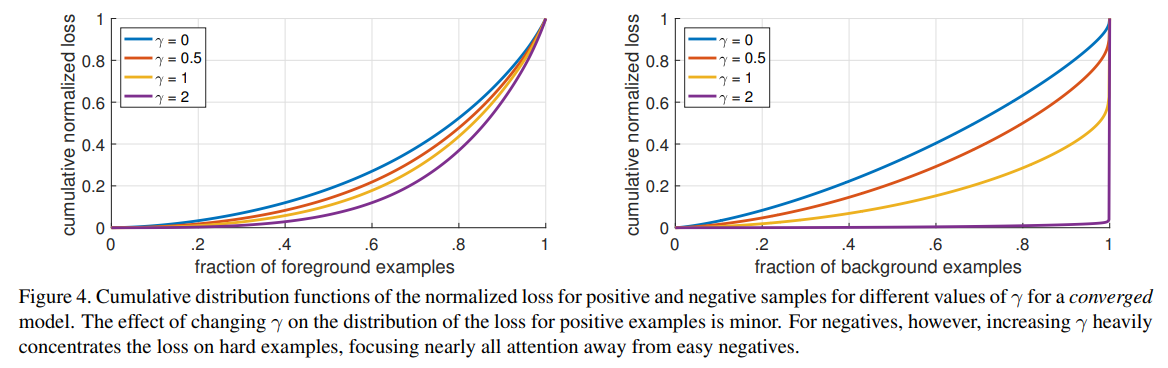
Figure4是对比forground和background样本在不同$\gamma$情况下的累积误差。纵坐标是归一化后的损失，横坐标是总的foreground或background样本数的百分比。可以看出$\gamma$的变化对正（forground）样本的累积误差的影响并不大，但是对于负（background）样本的累积误差的影响还是很大的（$\gamma=2$时，将近99%的background样本的损失都非常小）。

多分类focal loss的定义

个人感觉对于某一个样本，多分类的focal loss的定义如下：

$$\begin{eqnarray} loss=- \sum_{j=1}^J y_j \alpha_j (1-a_j)^\gamma \log a_j \end{eqnarray}$$

其中，$J$表示一共有$J$个类别，$y_j$为指示变量（0或1），如果样本的真实类标为$j$就是1，否则是0；$a_{j}$表示样本属于类别$j$的预测概率。$\alpha_j$为属于该类的权重，$\gamma$为focusing parameter。

Pytorch实现

class MultiFocalLoss(nn.Module):
    """多分类focal loss
    """
    def __init__(self, gamma=0, alpha=None, size_average=True):
        super(MultiFocalLoss, self).__init__()
        self.gamma = gamma
        self.alpha = alpha
        if isinstance(alpha, (float, int)): self.alpha = torch.Tensor([alpha, 1-alpha])
        if isinstance(alpha, list): self.alpha = torch.Tensor(alpha)
        self.size_average = size_average

    def forward(self, input, target):
        """
        Args:
            input: 模型的输入，取softmax后，表示对应样本属于各类的概率
            target: 真实类标
        """
        if input.dim() > 2:
            input = input.view(input.size(0), input.size(1), -1)  # N,C,H,W => N,C,H*W
            input = input.transpose(1, 2)    # N,C,H*W => N,H*W,C
            input = input.contiguous().view(-1, input.size(2))   # N,H*W,C => N*H*W,C
        target = target.view(-1, 1)

        logpt = F.log_softmax(input)
        # 沿给定轴dim，将输入索引张量index指定位置的值进行聚合。即取出真实类标对应的预测概率，logpt维度为[batch]
        logpt = logpt.gather(1, target)
        logpt = logpt.view(-1)
        # exp()对数据取指数，因为上面使用了log_softmax函数
        pt = Variable(logpt.data.exp())

        if self.alpha is not None:
            if self.alpha.type() != input.data.type():
                self.alpha = self.alpha.type_as(input.data)
            # 沿给定轴dim，将输入索引张量index指定位置的值进行聚合。即取出真实类标对应的alpha，at维度为[batch]
            at = self.alpha.gather(0, target.data.view(-1))
            logpt = logpt * Variable(at)

        loss = -1 * (1-pt)**self.gamma * logpt
        if self.size_average: 
            return loss.mean()
        else: 
            return loss.sum()

参考

图像分类任务中的损失
Focal Loss
pytorch之torch.gather方法